Il valore atteso
di P. J.
Quello che mi appresto a spiegare è un metodo basato sulla matematica e la statistica per il gioco della roulette. Saranno accennati argomenti di teoria combinatoria, eventi aleatori e variabili binominali.
Senza soffermandosi troppo sulla teoria, alquanto complessa e vasta, sarà riportato un esempio per la ricerca di un punto critico, da cui saranno tratte le conclusioni per impostare il gioco.
Teoria combinatoria
Calcoliamo le combinazioni con cui un’insieme di n numeri può creare una sequenza di lunghezza k :
Una combinazione di n oggetti di classe k ( k = n ) è il numero di modi in cui si possono disporre gli n oggetti in gruppi di k elementi, in maniera tale che ogni gruppo differisca dagli altri per la natura degli oggetti e non per il loro ordine.
Risulta banale dimostrare che 37 numeri possono disporsi in una combinazione di 37 numeri distinti per la loro natura a ordine variabile in una sola combinazione.
Infatti il coefficiente binomiale
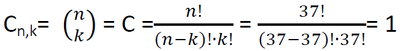
Calcoliamo invece ora quante combinazioni di 37 numeri si possono ottenere in 37 numeri anche ripetuti (l’ordine non conta):
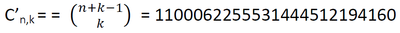
Procederemo con questa logica per calcolare le probabilità che determinate combinazioni si verifichino.
Inoltre ci serviremo di questi concetti per calcoli successivi.
Evento aleatorio
Vediamo ora cosa si intende con evento aleatorio:
Un evento si dice aleatorio o casuale se questi non è nelle condizioni per esprimere un giudizio certo sul suo verificarsi o meno.
Essi si dividono in elementari e composti, è un evento elementare che la pallina cadrà su un numero, è un evento composto che la pallina cadrà su un numero compreso fra 12 e 16.
Sia X una variabile aleatoria e siano x1,x2,…,xn i valori che essa può assumere.
Si dice densità o distribuzione di probabilità la funzione px : { x1,x2,…,xn } . R che a ogni valore del codominio di x associa la probabilita che X lo assuma.
Indicando con P( X = xk) la probabilità ha, nel caso finito, i seguenti valori :
px(x1) = P(X=x1), px (x2) = P(X=x2),…,px(xn) = P(X=xn).
Rappresentiamo la variabile aleatoria che rappresenta le probabilità che una certa combinazione si verifichi, in particolare una seria di lunghezza 15. Attribuendo ad ogni variabile la stessa probabilità di uscita, possiamo costruire la seguente tabella :

Con Xn =
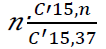
Procediamo con un esempio
Prendiamo in considerazione una seria lunga 15. Cominciamo con il calcolarci quante combinazioni con ripetizione potremo incontrare:
C’37,15 = 3188675231420
Ora calcoliamo quante combinazioni avremo di lunghezza 15 con l’uscita di 15 numeri distinti fra i 37 disponibili.
Eseguiamo i calcoli anche per 14,13,12,11,10,9,8. E calcoliamo le relative probabilità.
| Lunghezza | Combinazioni | Probabilità |
|---|---|---|
| 15 | 9.364.199.760 | 0,29% |
| 14 | 85.449.215.200 | 2,68% |
| 13 | 324.184.524.300 | 10,17% |
| 12 | 674.303.810.544 | 21,15% |
| 11 | 855.847.144.152 | 26,84% |
| 10 | 697.356.932.272 | 21,87% |
| 9 | 373.584.070.860 | 11,72% |
| 8 | 132.502.724.640 | 4,16% |
Possiamo notare come l’evento più probabile sia la serie composta da 11 numeri.
Facciamo attenzione però a non confondere il concetto di più probabile con il concetto di evento atteso.
Se calcoliamo la variabile aleatoria µ=E[X] noteremo infatti che ci indicherà come evento atteso una serie compostata da 10,93 numeri.
La variabile aleatoria è la media ponderata dei risultati dell'intervallo scelto, e cioè la somma del numero delle combinazioni per il proprio numero di riferimento, diviso il totale delle combinazioni.
nell'esempio:
(9.364.199.760*15+85.499.215.200*14+.......+132.502.724.640*8) / (9.364.199.760+85.499.215.200+.......+132.502.724.640)=10,93
Il punto critico
Abbiamo definito il valore che chiameremo punto critico per una serie da 8 a 15.
Conoscendo il punto critico sfrutteremo questo valore per impostare le nostre puntate.
Sapendo che le nostre probabilità sono direttamente proporzionali alla distanza da cui ci troviamo dal suddetto punto.
Non esiste una regola con cui determinare la convenienza o meno di inseguire il punto critico.
Si possono però esprimere dei valori mediante la probabilità a posteriori o frequentista
Ovvero con la legge empirica del caso la quale afferma che ripetendo una esperienza sempre nelle medesime condizioni, il valore della frequenza f osservata approssima quello della probabilità p valutata a priori, e l’approssimazione è tanto più precisa quanto più è elevato il numero delle prove eseguite.
Essa ci indica che l’intervallo da prendere in considerazione è + 3 e - 2 con approssimazione in eccesso. (intervallo empririco di fuori media derivato da test personali)
Ovvero 9 e 14.
NOTA: questo valore è differente per ogni punto critico, in generale si può affermare che la lunghezza della serie è direttamente proporzionale alle dimensioni dell’intervallo.
Concludiamo con un’ ultimo concetto.
La serie eccezionale
Se per i calcoli non è difficile trovare una serie di lunghezza 15 formata da due elementi ripetuti (ad es. 111111111115555), è alquanto improbabile riscontrare un evento simile nella realtà.
Il verificarsi di determinate condizioni abbassano sensibilmente le probabilità di successo e previsione della struttura di una serie.
Ecco allora che è importante riconoscere un evento eccezionale per fermare il gioco e riprenderlo al riassetto delle condizioni.
Consideriamo una serie eccezionale quando avviene per quattro volte la ripetizione di un numero all’interno di una qualsiasi serie.
Elaborazione di un sistema sfruttando il punto critico
Ricapitolando, ecco come la difficoltà della teoria si risolve in un metodo molto semplice.
- Calcoliamoci i punti critici per serie di lunghezza variabile
- Segniamo sul carnet della permanenza l’andamento del gioco, monitorando quanti numeri compongono le serie.
- Osserviamo di non essere in una serie eccezionale
- Confrontiamo l’andamento con il valore atteso, se ci troviamo a una distanza significativa da esso, imposteremo le puntate per l’inseguimento o la ripetizione dei numeri.
- Variamo l’entità del valore del pezzo in proporzione alla distanza da cui ci troviamo dal valore atteso
Questa è solo una tipologia di sistema che sfrutta il valore atteso.
Ricordo che il concetto di valore atteso è utile come suggerimento per individuare la selezione del momento di attacco, ma non definisce un vero e proprio sistema. Ognuno è libero di cucire il proprio sistema e la propria montante sfruttando il concetto di valore atteso/punto critico.
La teoria si presta bene però anche ad altri tipi di gioco, ad esempio, proviamo a pensare di giocare con un imbuto applicato sulle terzine servendoci dei risultati ipotetici del valore atteso per la selezione.
Ecco dimostrato come si può impostare un gioco basato sulla matematica.
Ma la stessa matematica ci pone in all’allerta con la definizione di evento aleatorio.
La certezza non fa parte di esso!
Simulazione software
In allegato vi propongo un software gratuito in cui è applicata questa strategia creato da un amico progammatore ( info@softwaroulette.it)
Istruzioni per il software:
- Apriamo la cartella software
- Apriamo l’applicazione ‘valore atteso’
- clicchiamo su impostazioni
- selezioniamo la nostra cassa iniziale convertita in pezzi
- selezioniamo 33 come ‘giri reset ciclo’
- clicchiamo carica dati per giocare con valori pre-impostati
- per aggiungere parametri o giocare con valori personali :
- impostiamo le boule da analizzare(lunghezza serie)
- impostiamo il numero di pieni che devono essere usciti
- impostiamo i pieni su cui puntare, 0 per puntare su i numeri non ancora usciti (inseguimento del valore atteso), 1,2,3 per puntare sui pieni usciti 1,2,3 per puntare su quelli già usciti (ripetizione).
ATTENZIONE per ogni valore bisogna reimpostare i parametri - selezioniamo l’entità della puntata. Valore convertito in pezzi
- clicchiamo su ‘aggiungi controllo’
- una volta inseriti i dati clicchiamo su ‘salva dati’ e chiudiamo la finestra
- selezioniamo sul tappeto di sinistra le boule uscite, su quello di destra compariranno le puntate.