Torna all'archivio

Triangolo di Pascal

Usare uno schema artimetico per aumentare progressivamente la puntata e recuperare con pochi colpi vinti un forte passivo

Blaise Pascal matematico francese del 17° secolo tra le diverse leggi enunciate (tra cui alcune sul calcolo della probabilità) creò una progressione aritmetica conosciuta appunto con il nome di “Triangolo di Pascal” illustrato qui sotto.

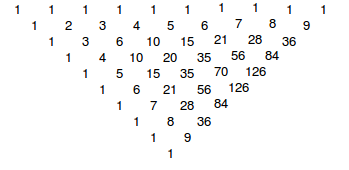
Che allineando le righe e le colonne assume questa forma

1	1	1	1	1	1	1	1	1	1
	1	2	3	4	5	6	7	8	9
		1	3	6	10	15	21	28	36
			1	4	10	20	35	56	84
				1	5	15	35	70	126
					1	6	21	56	126
						1	7	28	84
							1	8	36
								1	9
									1

La somma in verticale di ogni colonna forma esattamente la progressione geometrica in base 2 (La famosa Martingala)

128

256

512

Il triangolo funziona così. Ogni numero è la somma del numero sulla stessa riga della colonna precedente e quello imediatamente sempre nella colonna precedente. Ad esempio il 6 nella quinta colonna è dato dalla somma del 3 e del 3 della colonna precedente.

Il triangolo originale in realtà è completamente capovolto (vedi esempio sotto), questa sua diversa disposizione viene utilizzata perchè rende più facile e lineare il suo utilizzo in fase di gioco.

La principale e storica applicazione del triangolo di Pascal come montante alla roulette è la seguente:
Partendo dalla prima fila ci si sposta verso destra ad ogni colpo perso e si ritrona indietro verso sisnistra ad ogni colpo vinto. Quando si giunge al termine della riga si scende verso il basso di una riga e dall'estrema sinistra si riparte come in precedenza, così fino ad aver raggiunto un utile o il proprio obiettivo di cassa.

Analizzando il triangolo appare evidente che una progressione del genere è in realtà una somma di diverse progressioni, perchè la riga 1 gioca a tutti gli effetti a massa pari, la riga 2 è una D'Alembert pura aumenta un pezzo in perdita e lo diminuisce in vincita, mentre dalla riga tre in poi sono delle D'Alembert a passo 2, 3, 4, 5 , 6, 7 e 8.

Nell'esempio che segue ipotizziamo di essere arrivati ad un punto della partita in cui lo scarto tra colpi vinti e colpi persi è notevole e pertanto abbiamo completato sia la prima che la seconda riga e ci ritroviamo a giocare la terza riga con in cassa un passivo di 55 pezzi (10 prima riga e 45 della seconda).

Colpi	Risultato	Puntati	Vinti	Totale
1	Perso	1	0	-56
2	Perso	3	0	-59
3	Vinto	6	12	-53
4	Perso	3	0	-56
5	Vinto	6	12	-50
6	Perso	1	0	-51
7	Perso	3	0	-54
8	Perso	6	0	-60
9	Perso	10	0	-70
10	Vinto	15	30	-55
11	Vinto	10	20	-45
12	Vinto	6	12	-39
13	Perso	3	0	-42
14	Perso	6	0	-48
15	Vinto	10	20	-38
16	Vinto	15	30	-23
17	Vinto	21	42	-2
18	Vinto	28	56	26

Questa serie ci porta chiudere l'attacco recuperando alla terza riga tutto il passivo accumulato. Nel caso di uno scarto prolungato che porta a terminare tutte le righe del triangolo, si arriva a perdere 1023 pezzi

Come già detto questa è l'appliczione più classica, ma con tutti e 55 i numeri che formano il triangolo le possibilità di utilizzo da parte dei giocatori sono state e continueranno ad essere molteplici.